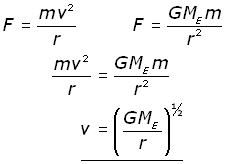Orbital Period Of A Satellite Calculator

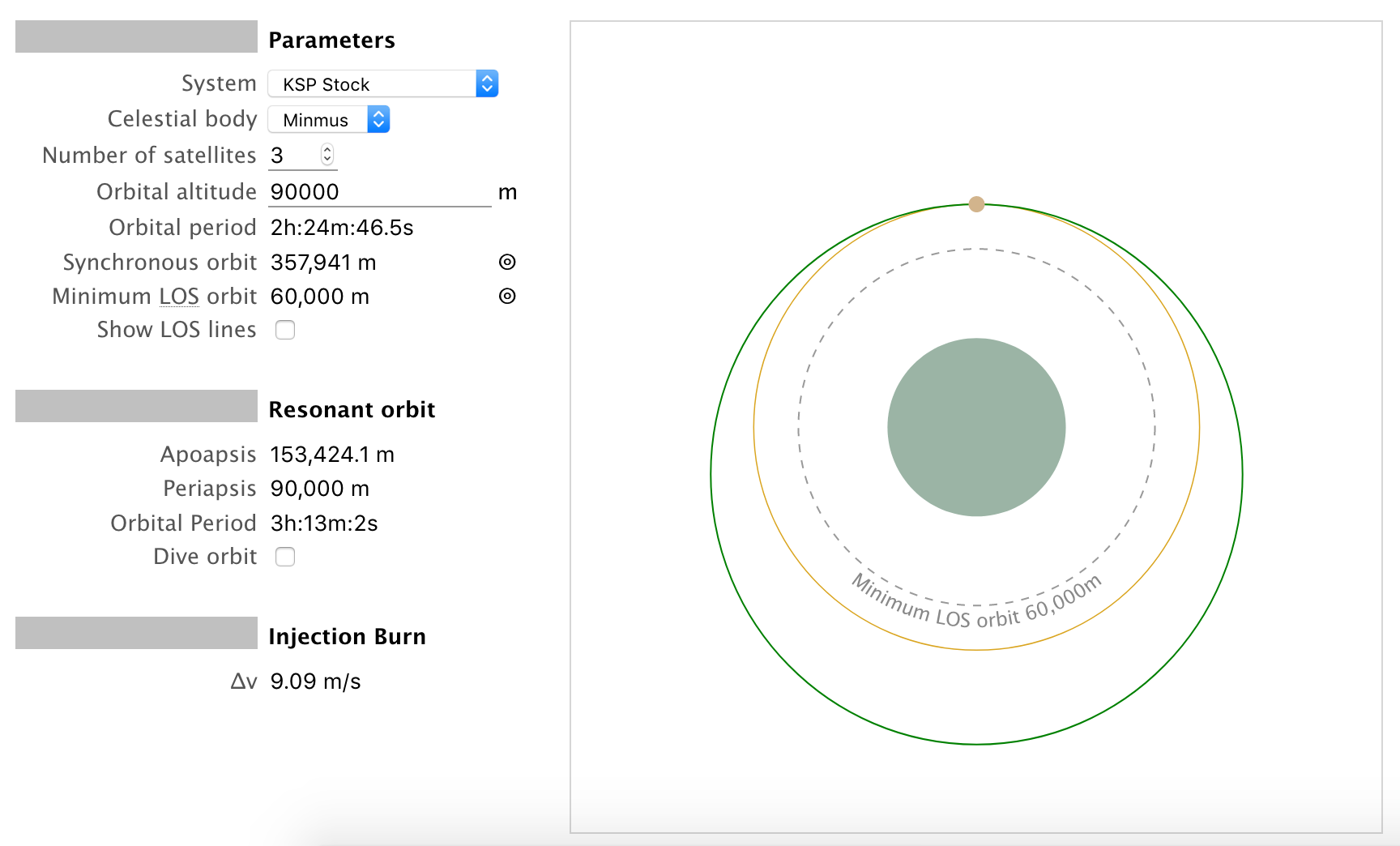
Resonant orbit calculator for kerbal space program.

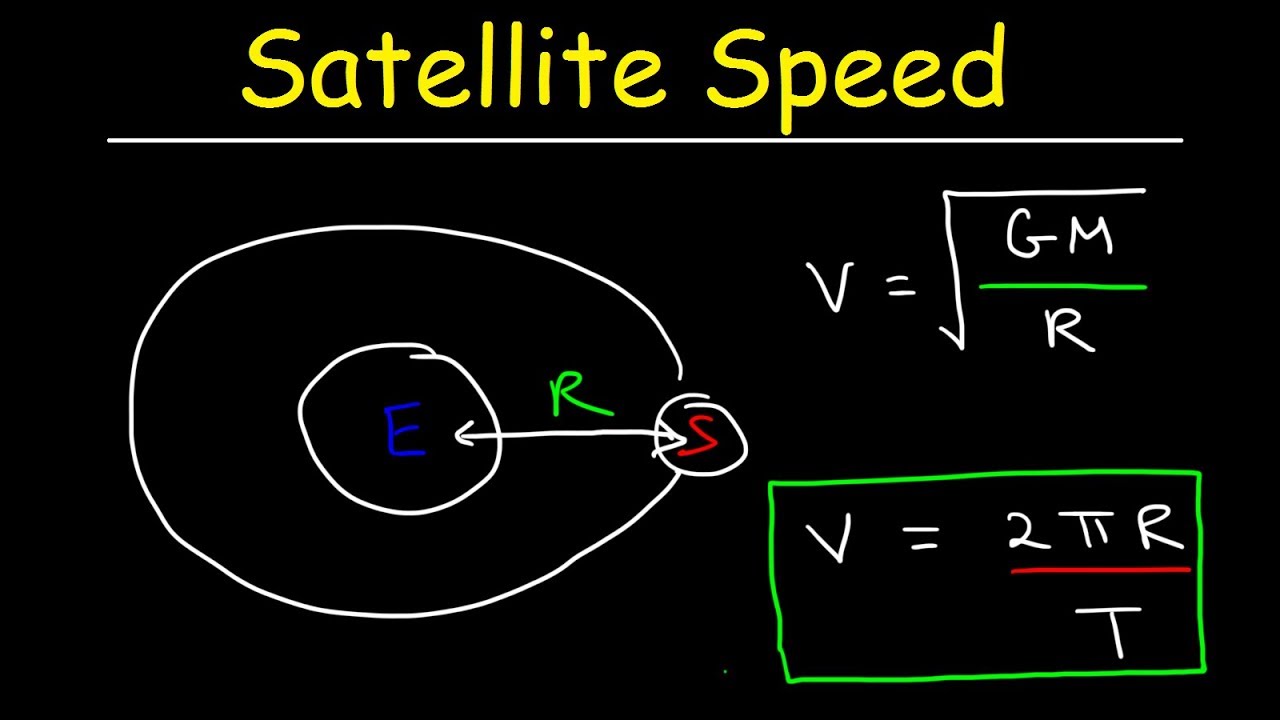
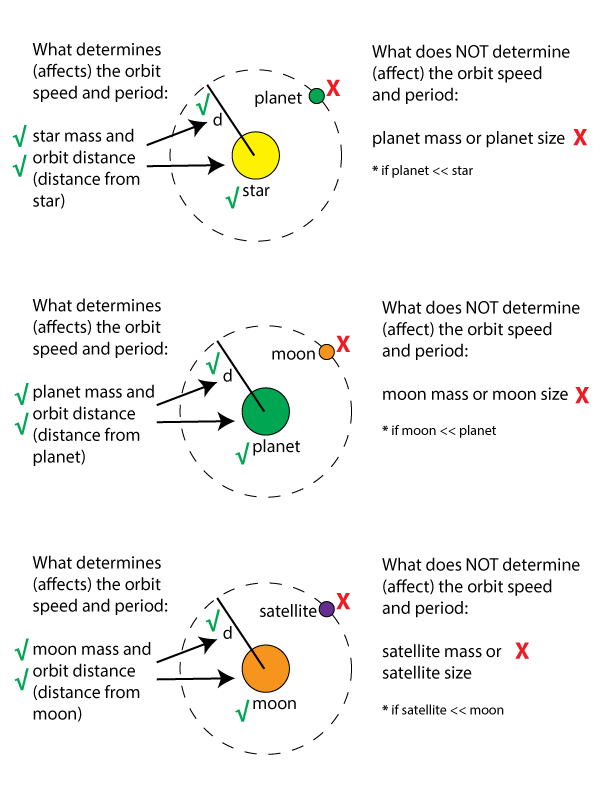
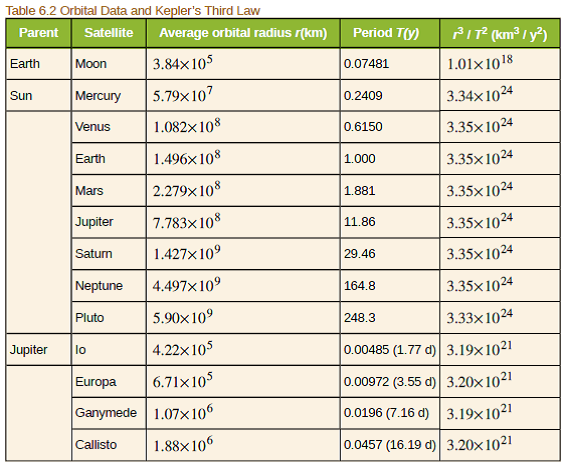
Orbital period of a satellite calculator. This calc determines the speed and orbital period of a satellite at a given height above average earth sea level. P is the orbital period. The period of a satellite is the time it takes it to make one full orbit around an object. The period of the earth as it travels around the sun is one year.

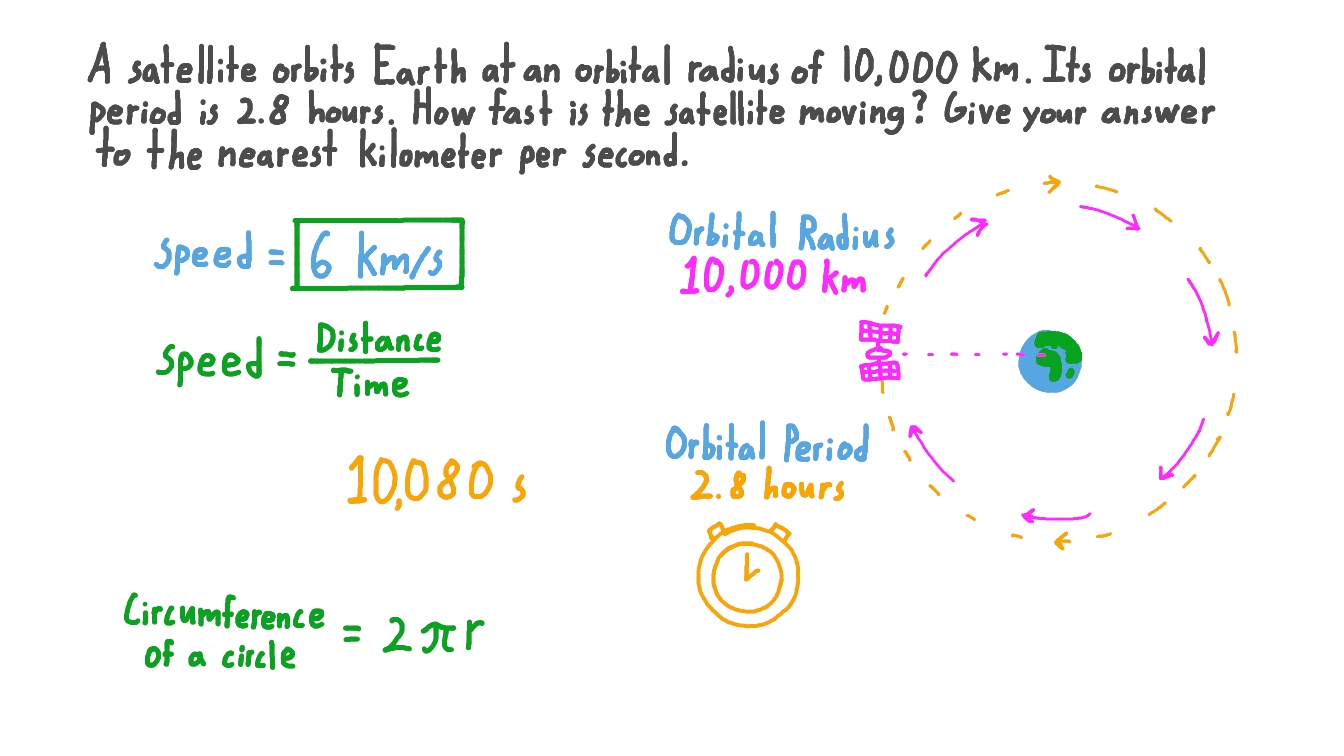
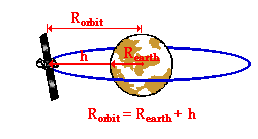
Calculates the orbital radius and period and flight velocity from the orbital altitude. The equation for orbital period is derived from newton s second law and newton s law of universal g. If you know the satellite s speed and the radius at which it orbits you can figure out its period. It now gives you an answer of 1 6195 hr.

This is useful for setting up things like commnet constellations. Astronomers discover a distant planet orbiting the sun. Mission control wishes to place a satellite in circular orbit above the earth. The calculator gives you an answer of 5830 318 s.

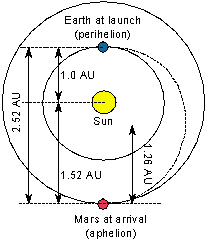
It s semi major axis is 1 light year. The injection δv value is the delta v required to move from the. Enter 12 h for p and 1 m earth for m and 1 r earth for r. Shows how to calculate the orbital period of a satellite.

The satellite must have a period of 12 hours. The orbital period is the time a given astronomical object takes to complete one orbit around another object and applies in astronomy usually to planets or asteroids orbiting the sun moons orbiting planets exoplanets orbiting other stars or binary stars. Enter 7000 km for a and 1 me for m. How many miles above the surface of the earth will this satellite orbit.

Calculate the resonant orbit needed for a carrier craft to inject craft it carries like satellites into equidistant positions of a shared circular orbit. Choose mi for the answer s units. The calculator gives you an. Orbit of a satellite calculator high accuracy calculation welcome guest.

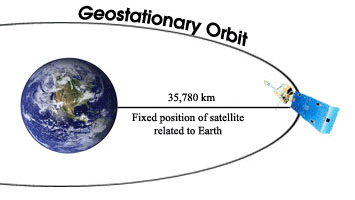
For objects in the solar system this is often referred to as the sidereal period determined by a 360 revolution of one celestial. This eliminates the need for continuous repositioning of satellite receiving dishes because even though the satellite is moving it stays in the same position relative to the earth. Velocity v square root g m r where g is a gravitational constant m is the mass of earth or other larger body and radius is the distance at which the smaller mass object is orbiting. Given that the earth s mass is 5 9736x10 24 kilograms and that the satellite s orbital period must be 86 400 seconds one day what altitude is required for a.

The formula for orbital speed is the following. Orbital height m metric pm nm microns µm mm cm km imperial mil 1 16 inch inches feet yards miles scientific planck bohrs angstrom light seconds light years au parsecs other points cubits fathoms rods.